Vectors
A scalar is a quantity that has magnitude. Scalars include quantities like length, mass, time and speed.
A vector is a quantity that has magnitude and direction. Vectors include quantities like displacement, weight, force and velocity. Vectors may be represented as $\vec{a}$, $\vec{b}$ and $\vec{c}$ or more simply as $\large{a, b}$ and $\large{c}$.
We will start by looking at vectors in two dimensions.
1. Unit Vectors
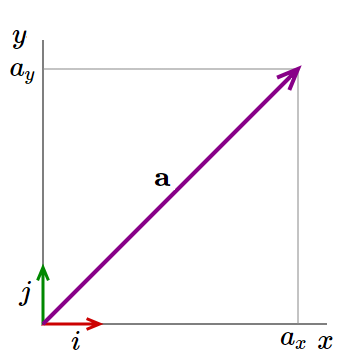
Vector $\large{a}$ has scalar components $a_x$ in the $x$ direction and $a_y$ in the $y$ direction.
Along the $x$-axis there is a vector which is one unit long called $i$ and along the $y$-axis there is a vector which is one unit long called $j$ so we can write $\large{a}$ $ = a_xi + a_yj$
The magnitude of $\large{a}$ can be found by $|a| = \sqrt{a_x^2+a_y^2} $.
2. 2D Direction Cosines
The angle between the vector $\large{a}$ and the $x$-axis is given by $\alpha=cos^{-1}(a_x/|a|)$. The angle between the vector $\large{a}$ and the $y$-axis is given by $\beta=cos^{-1}(a_y/|a|)$. These angles are called direction cosines. Obviously $\alpha+\beta=\pi/2$. These angle become more useful when we work with 3D vectors.
The direction cosines are often refered to as $l$ and $m$ where $l=cos(\alpha)$ and $m=cos(\beta)$.
$l=cos(\alpha)=a_x/|a|$
$m=cos(\beta)=a_y/|a|$
3. Vector Addition
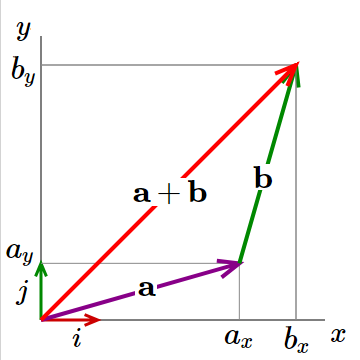
We can add two vectors, $\large{a}$ and $\large{b}$ by adding their respective components.
$\large{a}$ $ = a_xi + a_yj$ and $\large{b}$ $ = b_xi + b_yj$
so $\large{a} + \large{b}$ $ = (a_x + b_x)i + (a_y + b_y)j$
Example 3: Given $\large{a}$ $=3i+4j$ and $\large{b}$ $=2i+6j$ find $\large{a}+\large{b}$.
| $\large{a}$ | = | $3i+4j$ |
| $\large{b}$ | = | $2i+6j$ |
| $\large{a}+\large{b}$ | = | $(3+2)i+(4+6)j$ |
| = | $5i+10j$ |
4. Vector Subtraction
We can subtract vector $\large{b}$ from vector $\large{a}$ by subtracting the respective components.
$\large{a}$ $ = a_xi + a_yj$ and $\large{b}$ $ = b_xi + b_yj$
so $\large{a} - \large{b}$ $ = (a_x - b_x)i + (a_y - b_y)j$
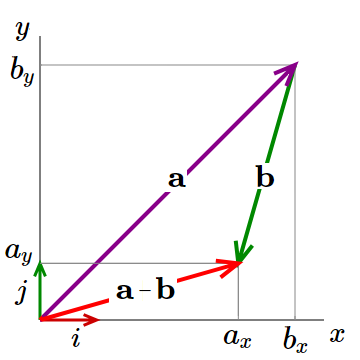
Example 4: Given $\large{a}$ $=4i+5j$ and $\large{b}$ $=6i+3j$ find $\large{a}-\large{b}$.
| $\large{a}$ | = | $4i+5j$ |
| $\large{b}$ | = | $6i+3j$ |
| $\large{a}-\large{b}$ | = | $(4-6)i+(5-3)j$ |
| = | $-2i+2j$ |
5. Vector Dot Product
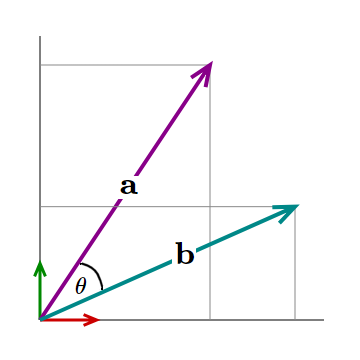
The vector dot product or scalar product multiplies vector $\large{a}$ by vector $\large{b}$ to give a scalar result.
$\large{a}\ . \large{b}$ $ = a_x . b_x + a_y . b_y $
Another way to calculate the vector dot product is
$\large{a}\ . \large{b}$ $ = |a|\ . |b|\ cos(\theta) $
Example 5a: Given $\large{a}$ $=2i-3j$ and $\large{b}$ $=i+4j$ find $\large{a}\ .\large{b}$
| $\large{a}$ | = | $2i-3j$ |
| $\large{b}$ | = | $i+4j$ |
| $\large{a}\ .\large{b}$ | = | $2\ . 1 + (-3)\ . 4$ |
| = | $-10$ |
Example 5b: Given $\large{a}$ $=(3, 10^{\circ})$ and $\large{b}$ $=(4, 70^{\circ})$ find $\large{a}\ .\large{b}$
| $\large{a}$ | = | $(3, 10^{\circ})$ |
| $\large{b}$ | = | $(4, 70^{\circ})$ |
| $\large{a}\ . \large{b}$ | = | $3\ . 4\ . cos(60)$ |
| = | $6$ |
In addition to the vector dot product there is a vector cross product. The vector cross product of $\large{a}$ and $\large{b}$ produces a vector that is perpendicular to the plane containing $\large{a}$ and $\large{b}$. See section 10
6. 3D Vectors
So far we have been looking at 2D vectors. To extend vectors to three dimensions we need to add an additional axis, the $z$-axis, which is perpendicular to both the $x$ and $y$ axes and, in this document, is pointing out of the page. The $z$-axis has a unit vector $j$ so the 3D vector $\large{a}$ may be represented as $\large{a}$ $ = a_xi + a_yj + a_zk$
7. 3D Vector Addition
Adding 3D vectors is similar to adding 2D vectors. All we have to do is add the components for the $z$ dimension.
$\large{a}$ $ = a_xi + a_yj + a_zk$ and $\large{b}$ $ = b_xi + b_yj + b_zk$
so
| $\large{a} + \large{b}$ | $=$ | $(a_x + b_x)i$ |
| $ + (a_y + b_y)j$ | ||
| $ + (a_z + b_z)k$ |
Example 7: Given $\large{a}$ $=6i+5j-4k$ and $\large{b}$ $=-10i+5j-5k$ find $\large{a}+\large{b}$.
| $\large{a}$ | = | $6i+5j-4k$ |
| $\large{b}$ | = | $-10i+5j-5k$ |
| $\large{a}+\large{b}$ | = | $(6-10)i+(5+5)j+(-4-5)k$ |
| = | $-4i+10j-9k$ |
See figure 7
8. 3D Vector Subtraction
We can subtract 3D vector $\large{b}$ from 3D vector $\large{a}$ by subtracting the respective 3D components.
$\large{a}$ $ = a_xi + a_yj + a_zk$ and $\large{b}$ $ = b_xi + b_yj + b_zk$
so
| $\large{a} - \large{b}$ | $=$ | $(a_x - b_x)i$ |
| $ + (a_y - b_y)j$ | ||
| $ + (a_z - b_z)k$ |
Example 8: Given $\large{a}$ $=6i+8j+5k$ and $\large{b}$ $=5i+14j-5k$ find $\large{a}-\large{b}$.
| $\large{a}$ | = | $6i+8j+5k$ |
| $\large{b}$ | = | $5i+14j-5k$ |
| $\large{a}-\large{b}$ | = | $(6-5)i+(8-14)j+(4-(-5))k$ |
| = | $i-6j+10k$ |
See figure 8
9. 3D Vector Dot Product
The 3D vector dot product or scalar product multiplies vector $\large{a}$ by vector $\large{b}$ to give a scalar result.
$\large{a}\ . \large{b}$ $ = a_x\ . b_x + a_y\ . b_y + a_z\ . b_z $
Another way to calculate the vector dot product is
$\large{a}\ . \large{b}$ $ = |a|\ . |b|\ cos(\theta) $
In 3D $|a|= \sqrt{a_x^2 + a_y^2 + a_z^2}$ and $|b|= \sqrt{b_x^2 + b_y^2 + b_z^2}$
Example 9a: Given $\large{a}$ $=-4i+6j+5k$ and $\large{b}$ $=5i+8j+4k$ find $\large{a}\ .\large{b}$
| $\large{a}$ | = | $-4i+6j+5k$ |
| $\large{b}$ | = | $5i+8j+4k$ |
| $\large{a}\ . \large{b}$ | = | $-4\ . 5 + 6\ . 8 + 5\ . 4$ |
| = | $48$ |
Example 9b: Find the angle between the two vectors from Example 9a.
| We know $\large{a}\ .\large{b}$ | = | $a_x\ . b_x + a_y\ . b_y + a_z\ . b_z$ |
| We also know $\large{a}\ .\large{b}$ | = | $|a|\ . |b|\ cos(\theta) $ |
| So we can write | ||
| $a_x\ . b_x + a_y\ . b_y + a_z\ . b_z$ | = | $|a|\ . |b|\ cos(\theta) $ |
| rearranging $cos(\theta)$ | = | $ \dfrac{a_x\ . b_x + a_y\ . b_y + a_z\ . b_z}{|a|\ . |b|} $ |
| which means $\theta$ | = | $ cos^{-1}(\dfrac{a_x\ . b_x + a_y\ . b_y + a_z\ . b_z}{|a|\ . |b|}) $ |
| $|a|$ | = | $ \sqrt{a_x^2 + a_y^2 + a_z^2}$ |
| = | $ \sqrt{(-4)^2 + 6^2 + 5^2}$ | |
| = | $ \sqrt{77}$ | |
| $|b|$ | = | $ \sqrt{b_x^2 + b_y^2 + b_z^2}$ |
| = | $ \sqrt{5^2 + 8^2 + 4^2}$ | |
| = | $ \sqrt{105}$ | |
| $\theta$ | = | $ cos^{-1}(\dfrac{-4\ . 5 + 6\ . 8 + 5\ . 4$}{\sqrt{77}\ . \sqrt{105}}) $ |
| = | $ cos^{-1}(\dfrac{48}{89.92}) $ | |
| = | $ 1.01 $ rad or $57.74^{\circ}$ | |
10. Vector Cross Product
The vector cross product is the product of two vectors $\large{a} \times \large{b}$ that results in a vector. The resultant vector is perpendicular to the plane containing $\large{a}$ and $\large{b}$ and is in the direction a right hand thread or corkscrew would travel when rotated from $\large{a}$ to $\large{b}$. This means $\large{a} \times \large{b}$ is on the same unit vector as $\large{b} \times \large{a}$ but points in the opposite direction.
There are two ways to calculate the vector cross product:
- $\large{a} \times \large{b}$ $ = |a|\ |b|\ sin(\theta) . n$
where $\theta$ is the angle between $\large{a}$ and $\large{b}$ and $n$ is the right handed unit vector perpendicular to the plane containing $\large{a}$ and $\large{b}$ and pointing in the direction of a right hand thread or corkscrew rotating from $\large{a}$ to $\large{b}$. - $\large{a} \times \large{b}$ $ = \begin{vmatrix} i & j & k \\ a_x & a_y & a_z \\ b_x & b_y & b_z \notag \end{vmatrix} $
Expanding the determinant we get$\large{a} \times \large{b}$ $ = (a_y b_z - a_z b_y)i - (a_x b_z - a_z b_x)j + (a_x b_y - a_y b_x)k$
Note: Remember the signs rule for expanding determinants which changes the sign of the $j$ term.
Example 10: Given $\large{a}$ $=-4i+6j+5k$ and $\large{b}$ $=5i+8j-4k$ find $\large{a} \times \large{b}$.
| $\large{a}$ | = | $-4i+6j+5k$ |
| $\large{b}$ | = | $5i+8j+4k$ |
| $\large{a} \times \large{b}$ | = | $\begin{vmatrix} i & j & k \\ -4 & 6 & 5 \\ 5 & 8 & 4 \notag \end{vmatrix} $ |
| = | $i(24-40)$ | |
| $-j(-16-25)$ | ||
| $+k(-32-30)$ | ||
| = | $-16i+41j-62k$ |
See figure 10
11. 3D Direction Cosines
An alternative way to specify a vector is give its magnitude and the angle it makes with each of the axes. The three angles are usually called $\alpha, \beta$ and $\gamma$ (alpha, beta and gamma) where $\alpha$ is the angle between the vector and the $x$-axis, $\beta$ is the angle between the vector and the $y$-axis and $\gamma$ is the angle between the vector and the $z$-axis.
The cosines are often called $l$, $m$ and $n$ where $l=cos(\alpha)$, $m=cos(\beta)$ and $n=cos(\gamma)$
| $l$ | $\ =\ $ | $cos(\alpha)$ | $\ =\ $ | $a_x/|a|$ |
| $m$ | $\ =\ $ | $cos(\beta)$ | $\ =\ $ | $a_y/|a|$ |
| $n$ | $\ =\ $ | $cos(\gamma)$ | $\ =\ $ | $a_z/|a|$ |
Example 11: Given $\large{a}$ $=4i+6j+5k$ find the direction cosines.
| $\large{a}$ | = | $4i+6j+5k$ |
| $| \large{a}|$ | = | $\sqrt{16 + 36 + 25}$ |
| $8.77$ | ||
| $cos \alpha$ | = | $4/8.77=0.46\ rad$ |
| $cos \beta$ | = | $6/8.77=0.68\ rad$ |
| $cos \gamma$ | = | $5/8.77=0.57\ rad$ |
| So $4i+6j+5k$ | = | $[0.46,0.68,0.57]$ |