Integration
Integration may be seen as the inverse process of differentiation. If we differentiate $y=4x^3+5$ we get $dy/dx=12x^2$ so if we integrate $12x^2$ we should get something like $4x^3+5$.
When we differentiate $4x^3$ we multiply the coefficient, $4$, by the exponent, $3$, then reduce the exponent by $1$. $\dfrac{d}{dx}(4x^3) = 3 \times 4x^2 = 12x^2$.
To integrate $12x^2$ we increase the exponent by $1$ then divide by the new exponent. $\int 12x^2 dx = 12x^3 / 3 = 4x^3$
But what happened to the $5$?
When we differentiate a constant like $5$ we get zero. When we integrate zero we don't know what we get so we call it $C$, the constant of integration. We won't know the value of $C$ until we know the boundary conditions.
1 Integrating Polynomial Expressions
If we differentiate the polynomial $y=ax^3+bx^2+cx+d$
we get $dy/dx=3ax^2+2bx+c$
We have differentiated the expression one term at a time.
$cx$ could be written as $cx^1$ when we reduce the exponent by $1$ we get $x^0$ which it equal to $1$ so $\dfrac{d}{dx}(cx)=c$.
$d$ could be written as $dx^0$. When we multiply by the exponent of $x$, which is $0$, the term becomes $0$ so $\dfrac{d}{dx}(d)=0$.
The process of differentiation was to multiply each coefficient by the exponent of the $x$ term and then reduced the exponent by $1$.
The process of integration is to increase the exponent of each $x$ term by $1$ then divide the coefficient by the new exponent.
Starting with $\dfrac{dy}{dx}=3ax^2+2bx+c$ we increase the exponent of each term by $1$ then divide the coefficient by the new exponent.
This gives us $y=ax^3+bx^2+cx$. Notice we have lost the $d$ term. We need to add the constant of integration $C$ until we know what value the constant term holds.
The result is $\int \dfrac{dy}{dx}dx = ax^3+bx^2+cx+C$ which is similar but not identical to the original expression.
Sanity Check
The best sanity check for integration is differentiation. When you have integrated an expression always differentiate it to see you get back to the starting point.
| Example 1 | ||
| Integrate $y=12x^3+6x^2+4x+5$ with respect to $x$ | ||
| $\int y\ dx$ | $=$ | $\int 12x^3+6x^2+4x+5)dx$ |
| $=$ | $ \dfrac{12x^4}{4}+\dfrac{6x^3}{3}+\dfrac{4x^2}{2}+5x+C$ | |
| $=$ | $3x^4+2x^3+2x^2+5x+C$ | |
| Sanity Check | ||
| Differentiate $f(x)=3x^4+2x^3+2x^2+5x+C$ | ||
| $\dfrac{d}{dx}(f(x))$ | $=$ | $4 \times 3x^3+3 \times 2x^2+2 \times 2x+5$ |
| $=$ | $12x^3+6x^2+4x+5$  | |
This is called an indefinite integral because we do not know the value of $C$. We keep $C$ until we can evaluate it by using the boundary conditions.
2 Table of Common Standard Integrals
The following table has a column of functions of $x$ ($y=f(x)$) on the left. The right hand column contains the integrals of the functions with respect to $x$ ($ \int f(x) dx=F(x)$).
| $y=f(x)$ | $ \int f(x) = F(x)$ |
|---|---|
| $x^n$ | $ \dfrac{x^{n+1}}{n+1}+C$ |
| $x^{-1}$ | $ ln(x)+C$ for $x>0$ |
| $ ln(-x)+C$ for $x<0$ | |
| $sin(ax)$ | $-cos(ax)/a+C$ |
| $cos(ax)$ | $sin(ax)/a+C$ |
| $tan(ax)$ | $ln(sec(ax))/a+C$ |
| $e^{ax}$ | $e^{ax}/a+C$ |
| $ln(ax)$ | $x(ln(ax)-1)+C$ |
| Example 2 | ||
| Integrate $y=cos(2x)$ with respect to $x$ | ||
| $\int y\ dx$ | $=$ | $\int cos(2x)dx$ |
| $=$ | $\dfrac{sin(2x)}{2}+C$ | |
| Sanity Check | ||
| Differentiate $f(x)=\dfrac{sin(2x)}{2}+C$ | ||
| $\dfrac{d}{dx}(f(x))$ | $=$ | $2 \times \dfrac{cos(2x)}{2}$ |
| $=$ | $cos(2x)$  | |
| Example 3 | ||
| Integrate $y=sin(3x)$ with respect to $x$ | ||
| $\int y\ dx$ | $=$ | $\int sin(3x)dx$ |
| $=$ | $\dfrac{-cos(3x)}{3}+C$ | |
| Sanity Check | ||
| Differentiate $\dfrac{-cos(3x)}{3}+C$ | ||
| $\dfrac{d}{dx}(f(x))$ | $=$ | $3 \times \dfrac{sin(3x)}{3}$ |
| $=$ | $sin(3x)$  | |
| Example 4 | ||
| Integrate $y=e^{3x}$ with respect to $x$ | ||
| $\int y\ dx$ | $=$ | $\int e^{3x}dx$ |
| $=$ | $e^{3x}/3+C$ | |
| Sanity Check | ||
| Differentiate $e^{3x}/3+C$ | ||
| $\dfrac{d}{dx}(f(x))$ | $=$ | $3 e^{3x}/3$ |
| $=$ | $e^{3x}$  | |
3 Integration by Substitution
Expressions that include a function of a linear factor may be integrated using a substitution.
If we want to integrate $(3x+4)^5$ we let $3x+4=u$.
Differentiating we get $du/dx=3$ so $dx=du/3$.
Substituting into the integral we get
| $I$ | $=$ | \( \int (3x+4)^5dx \) |
| $=$ | $\dfrac{1}{3}\int u^5du$ | |
| $=$ | $ \dfrac{1}{3} \dfrac{u^6}{6}+C $ | |
| $=$ | $ \dfrac{(3x+4)^6}{18}+C $ |
| Example 5 | ||
| $I=\int (4x-3)^3 dx$ | ||
| Let $u = 4x-3$ so $du/dx = 4$ or $dx = du/4$ | ||
| $I$ | $=$ | $\dfrac{1}{4}\int u^3 du$ |
| $=$ | $\dfrac{1}{4}(\dfrac{u^4}{4})+C$ | |
| Substituting $u = 4x-3$ | ||
| $I$ | $=$ | $\dfrac{(4x-3)^4}{16}+C$ |
| Sanity Check | ||
| $\dfrac{d}{dx}(\dfrac{(4x-3)^4}{16}+C)$ | $=$ | $\dfrac{4(4x-3)^3}{16} \times 4$ |
| $=$ | $(4x-3)^3$  | |
| Example 6 | ||
| $I=\int \dfrac{4}{2x-3} dx$ | ||
| Let $u = 2x-3$ so $\dfrac{du}{dx} = 2$ or $dx = \dfrac{1}{2}du$ | ||
| $I$ | $=$ | $4\int \dfrac{1}{2u} du$ |
| $=$ | $2\int \dfrac{1}{u} du$ | |
| $=$ | $2 ln(u)+C$ | |
| Substituting $u = 2x-3$ | ||
| $=$ | $2 ln(2x-3)+C$ | |
| Sanity Check | ||
| Differentiate $\dfrac{d}{dx}(2ln(2x-3)+C)$ | ||
| $\dfrac{d}{dx}(2ln(2x-3))$ | $=$ | $2 \times \dfrac{1}{2x-3} \times 2$ |
| $=$ | $\dfrac{4}{2x-3}$  | |
4 Integration by Partial Fractions
An expression of the form $I=\int \dfrac{ax+b}{cx^2+dx+e}dx$ cannot be integrated using the table of standard integrals but we may be able to simplify the expression using partial fractions. First we need to see whether we can factorise the denominator. If we can then we can seperate the quadratic fraction into linear fractions which we can then integrate.
| Example 7 | ||
| Integrate $I=\int \dfrac{2x+23}{2x^2+x-10}dx$ | ||
| First see if we can factorise the denominator. | ||
| You can probably see that $2x^2+x-10=(2x+5)(x-2)$ so we can write | ||
| $\dfrac{2x+23}{2x^2+x-10}$ | $=$ | $\dfrac{A}{2x+5}+\dfrac{B}{x-2}$ |
| where $A$ and $B$ are unknown constants. | ||
| Putting the right hand side over a common denominator we get | ||
| $=$ | $\dfrac{A(x-2)+B(2x+5)}{(2x+5)(x-2)}$ | |
| Cancelling the denominators we get | ||
| so $2x+23$ | $=$ | $A(x-2)+B(2x+5)$ (1) |
| If we let $x=2$ we get $4+23=B(4+5)$ so $B=3$ | ||
| Now let $x=-5/2$ then $-5+23=A(-5/2-2)$ so $A=-4$ | ||
| We have found values for $A$ and $B$ so we can write | ||
| $\int \dfrac{2x+23}{2x^2+x-10}dx$ | $=$ | $\int \dfrac{3}{x-2}dx - \int \dfrac{4}{2x+5}dx+$ |
| Notice we have written the $B$ term first because the $A$ term is negative. | ||
| Sanity Check | ||
| Before we continue we should put the values of $A$ and $B$ into equation (1) to check the values are correct. | ||
| $A(x-2)+B(2x+5)$ | $=$ | $-4(x-2)+3(2x+5)$ |
| $=$ | $-4x+6x+8+15$ | |
| $=$ | $2x+23$ | |
| This is the same as the left hand side of equation (1) so we can continue. | ||
| Integrating we get $I$ | $=$ | $\int \dfrac{3}{x-2}dx - \int \dfrac{4}{2x+5}dx+$ |
| $=$ | $3ln(x-2) - 4 ln(2x+5)/2 + C$ | |
| $=$ | $3 ln(x-2) - 2 ln(2x+5)+C$ | |
5 Integration by Parts
| We know | ||
| $\dfrac{d}{dx}(uv)$ | $=$ | $v\dfrac{du}{dx}+u\dfrac{dv}{dx}$ |
| If we integrate this equation we get | ||
| $uv$ | $=$ | $\int v\dfrac{du}{dx}dx+\int u\dfrac{dv}{dx}dx$ |
| Rearranging this we get | ||
| $\int u\dfrac{dv}{dx}dx$ | $=$ | $uv-\int v\dfrac{du}{dx}dx$ |
| This equation can be used to solve a range of otherwise difficult problems. For example, let us integrate $x sin(x)$. | ||
| Example 8 | ||
| Integrate $I=\int x sin(x) dx$ | ||
| Let $u=x$ and $dv=sin(x)$. | ||
| Differentiate $u$ and integrate $dv$ to get $du=dx$ and $v=-cos(x)$ so we can write | ||
| $\int x sin(x) dx$ | $=$ | $-x cos(x)-\int (-cos(x))dx$ |
| $=$ | $-x cos(x)+sin(x) +C$ | |
| $=$ | $sin(x)-x cos(x)+C$ | |
| Sanity Check | ||
| Differentiate $sin(x)-x cos(x)+C$ | ||
| $=$ | $cos(x)-cos(x)+xsin(x)$ | |
| $=$ | $xsin(x)$  | |
6 Definite Integration
Definite integration is where we integrate between two limits giving us the area between the curve and the axis.
Consider the equation $y=x^2+2$. If we integrate this between $x=1$ and $x=2$ we will get the shaded area shown in figure 1
$I = \int^2_1 x^2+2\ dx$
Integrating we get
$I = \dfrac{x^3}{3}+2x\ \Biggr|_{1}^{2}$
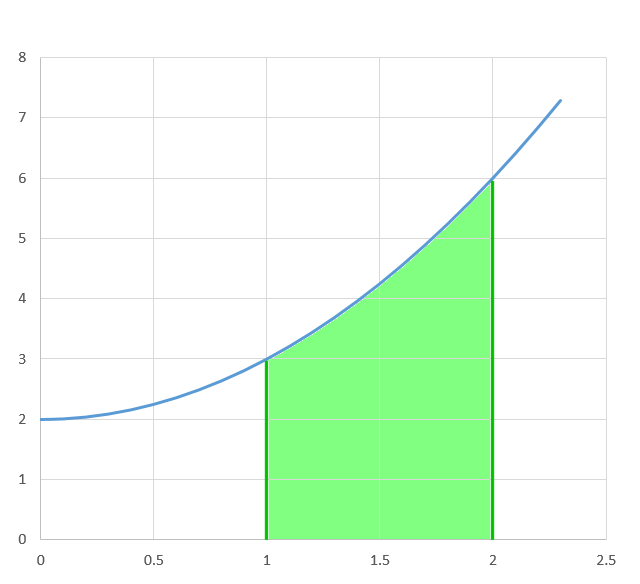
Notice there is no constant of integration. That is because we have the limits $x=1$ and $x=2$ which removes any uncertainty.
To evaluate the integral we find the value when we replace $x$ with $2$, the upper limit, and then subtract the value when we replace $x$ with $1$, the lower limit.
$I = \dfrac{x^3}{3}+2x\ \Biggr|_{1}^{2}$
$I = \dfrac{2^3}{3} + 2 \times 2 - (\dfrac{1^3}{3} + 2 \times 1)$
$I = \dfrac{8}{3}+4-(\dfrac{1}{3}+2) = \dfrac{20-7}{3} = \dfrac{13}{3}$
So the shaded area in figure 1 between $x^2+2$, $x=1$, $x=2$ and the $x$-axis is $13/3$.
| Example 9 | ||
| Integrate $\int^{\pi/2}_0 cos(\theta)\ d\theta$ | ||
| $I$ | $=$ | $\int^{\pi/2}_0 cos(\theta)\ d\theta$ |
| $=$ | $sin(\theta)\ \Biggr|_{0}^{\pi/2}$ | |
| $=$ | $1 - 0 = 1$ | |
What would happen if we integrated $cos(\theta)$ from $\pi/4$ to $3\pi/4$, the shaded area on figure 2?
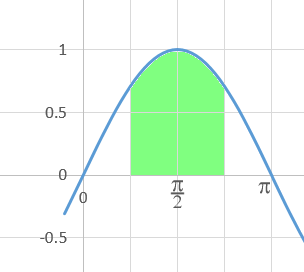
| $I$ | $=$ | $sin(\theta)\ \Biggr|_{\pi/4}^{3\pi/4}$ |
| $=$ | $0.7071 - 0.7071 = 0$ |
which is clearly not right, the shaded area is not zero.
What we have to do in cases like this is notice the area is symmetrical about $\pi/2$ so we can calculate the area between $\pi/4$ and $\pi/2$ and then double it.
| $I$ | $=$ | $sin(\theta)\ \Biggr|_{\pi/4}^{\pi/2}$ |
| $=$ | $1 - 0.7071$ | |
| So the area $= 2 \times 0.2929 = 0.59$ | ||
7 Volumes of Revolution
7.1 Cone
Imagine a straight line from the origin $y=mx$. If we rotate the line about the $y$-axis we will get a cone with its apex at the origin.
What is the volume of the cone?
To find the volume of the cone we first look at the area of a disc parallel to the $xz$ plane. The radius is $x$ so the area is $\pi x^2$. If we integrate from $y=0$ to $y=h$ we will find the volume.
$V=\int_0^h \pi x^2 dy$
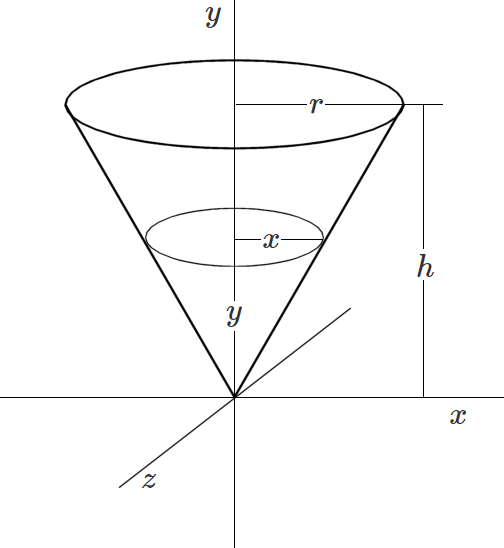
By similar triangles we can see $\dfrac{x}{y} = \dfrac{r}{h}$ so we can write $x= \dfrac{ry}{h}$. Substituting for $x$ in our equation for volume we get
| $V$ | $=$ | $\int_0^h \dfrac{\pi r^2 y^2}{h^2} dy$ |
| $=$ | $\dfrac{\pi r^2 y^3}{3h^2}\ \Biggr|_{0}^{h}$ | |
| $=$ | $\frac{1}{3}\pi r^2 h$ | |
| So the volume of a cone is given by $\frac{1}{3}\pi r^2 h$ | ||
7.2 Sphere
We can use a similar technique to find the volume of a sphere. As before we look at the area of a disc parallel to the $xz$ plane. The radius is $x$ so the area is $\pi x^2$. If we integrate $\pi x^2$ from $y=-r$ to $y=r$ we will find the volume. Before we do that we need to find $x$ in terms of $y$.
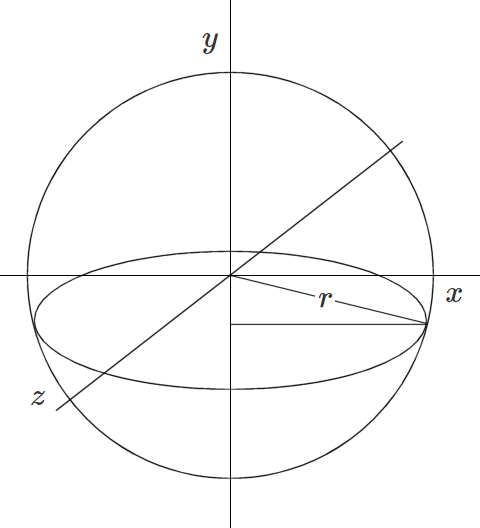
| We know $r^2=x^2+y^2$ so we can write $x^2 = r^2 - y^2$. Substituting for $x^2$ in the integral we get: | ||
| $V$ | $=$ | $\int_{-r}^r \pi (r^2-y^2) dy$ |
| $=$ | $\pi (r^2y-y^3/3)\ \Biggr|_{-r}^{r} $ | |
| $=$ | $\pi ((r^3-r^3/3)-(-r^3+r^3/3))$ | |
| $=$ | $\pi ((2r^3/3)-(-2r^3/3))$ | |
| $=$ | $\dfrac{4}{3}\pi r^3$ | |
7.3 Liquid in a Sphere
Sometimes we are interested in the volume of liquid in a sphere. In that case it is better to set the origin at the bottom of the sphere rather than at the geometric centre.
| Looking at figure 5 we can see $r^2=x^2+(r-y)^2$ so we can write $x^2 = 2ry - y^2$. | ||
| Substituting for $x^2$ in the integral we get: | ||
| $V$ | $=$ | $\int \pi (2ry-y^2) dy$ |
| $=$ | $\pi (2ry-y^3/3)+C$ | |
| When $y=0, V=0$ which means $C=0$ so we can write: | ||
| $V$ | $=$ | $\pi (2ry-y^3/3)$ |
| For a sanity check try inserting values for $y=0, y=r$ and $y=2r$. | ||

Volume of a cone is $\dfrac{\pi r^2 h}{3}$
Volume of a sphere is $\dfrac{4}{3}\pi r^3$
Volume of liquid in a sphere is $\pi (2ry-y^3/3)$